Can Zero-shot RL enable test time safety?
June 01, 2025
To develop a truly generalized agent, it is essential to enable it to perform well on multiple unseen tasks without training a separate agent for each scenario. In standard reinforcement learning (RL), an agent trained on a single, fixed reward function typically lacks the ability to generalize beyond that task. Zero-shot RL addresses this challenge by training agents without access to explicit reward signals and aims to produce policies that can be conditioned on any given reward instantly at test time. This capability is particularly valuable in offline RL settings, where agents are pretrained on large-scale datasets that do not contain reward labels.
Zero-shot RL shows potential for producing general-purpose, reusable agents that can be deployed in real-world environments without requiring additional data collection, which is often expensive or dangerous. Recent advancements in zero-shot RL have decoupled environment dynamics from the reward function, enabling generalization across tasks. However, a critical limitation of existing approaches is the lack of safety guarantees, which is crucial for real-world deployment. Unlike standard safe RL settings–where unsafe behaviors can be corrected during training–zero-shot RL agents must satisfy safety constraints immediately when executing a new policy.
This raises an important question: if the zero-shot RL problem is to adapt to any reward, can it also adapt to any safety constraint?
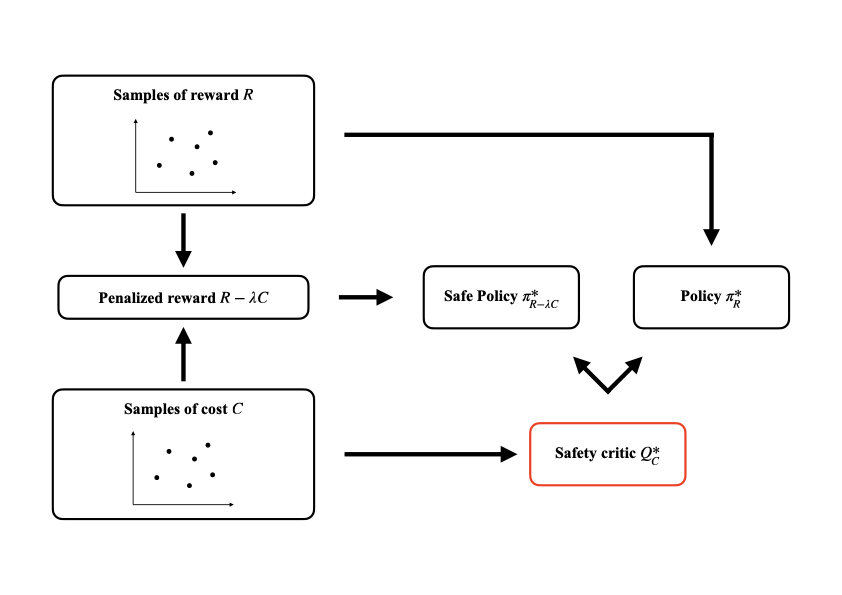
I propose FB-safe, a zero-shot safety method that extends the Forward-Backward (FB) representations introduced by Touati et al. (2021) to incorporate safety. My approach enables agents to adapt to safety constraints at test time by leveraging generalized Q-functions that span both reward and cost signals. This eliminates the need for further exploration or fine-tuning and allows for safe, efficient deployment in offline safe RL scenarios. I evaluate FB-safe against prior state-of-the-art methods and show that it balances task performance and safety competitively. The results indicate that the zero-shot RL problem can be extended to a zero-shot safety problem, offering a novel perspective on how to approach safety in RL without task-specific training.
Constrained Markov Decision Process (CMDP)
To incorporate safety into zero-shot RL, I consider a Constrained Markov Decision Process (CMDP). During training, a reward-free MDP defined by the tuple $(S, A, P, \gamma)$ is given, where $S$ is the state space, $A$ is the action space, $P: S \times A \times S \rightarrow \mathbb{R}$ is the transition probability, and $\gamma \in [0, 1)$ is the discount factor.
At test time, I am given a reward function $R: S \rightarrow \mathbb{R}$ and a cost function $C: S \rightarrow \mathbb{R}_{\ge 0}$ that penalizes unsafe behavior, forming a CMDP $(S, A, P, R, C, \gamma)$. The main goal for the policy in a CMDP is to maximize expected return while ensuring that the expected cumulative cost satisfies an upper bound $\epsilon$:
\[\pi^*_{R,C} = \arg\max_\pi \mathbb{E}^\pi\left[\sum_{t=0}^{\infty} R(s_t)\right] \quad \text{s.t.} \quad \mathbb{E}^\pi\left[\sum_{t=0}^{\infty} C(s_t, a_t)\right] \le \epsilon.\]FB representation
For the training phase, I build on the FB framework. The successor measure is defined as
\[\begin{aligned} M^\pi_z(s_0, a_0, s) &= \sum_{t \ge 0} \gamma^t \Pr(s_{t+1} = s \mid s_0, a_0, \pi), \end{aligned}\]and is approximated in a finite-dimensional space by using two parametric functions: a forward mapping $F_z^\top: S \times A \rightarrow \mathbb{R}^d$ and a backward mapping $B: \mathbb{R}^d \rightarrow S$ such that
\[\begin{aligned} M^\pi_z(s_0, a_0, s') = F(s_0, a_0, z)^\top B(s')\rho(ds'), \end{aligned}\]where $\rho$ is the data distribution. For any reward function $R$, I estimate the latent reward vector using a small number of samples:
\[z_R = \mathbb{E}_\rho[R(s) B(s)].\]The optimal Q-function and policy parameterized by $z_R$ are given by
\[\begin{aligned} Q_R^*(s, a) &= F(s, a, z_R)^\top z_R, \\ \pi_R^*(s) &= \arg\max_a F(s, a, z_R)^\top z_R. \end{aligned}\]Training the forward and backward functions uses TD learning with the loss
\[\begin{aligned} L_{\text{FB}} =& \mathbb{E}_{(s_t, a_t, s_{t+1}) \sim \rho} \Big[\big(F(s_t, a_t, z)^\top B(s') - \gamma \, \bar{F}(s_{t+1}, \pi_z(s_{t+1}), z)^\top \bar{B}(s')\big)^2\Big] \\ &- 2 \mathbb{E}_{\rho, z}\left[F(s_t, a_t, z)^\top B(s_{t+1})\right], \end{aligned}\]where $\bar{F}, \bar{B}$ are target networks and $\pi_z$ is a deterministic actor that is trained jointly, similar to DDPG (Lillicrap et al., 2015).
Jeen et al. (2024) showed that adding a conservative learning term improves offline RL performance:
\[\begin{aligned} L_{\text{VC}} = &\mathbb{E}_{s \sim \rho, \, a \sim \mu(\cdot \mid s)} \big[F(s, a, z)^\top z\big] \\ &- \mathbb{E}_{(s, a) \sim \rho} \big[F(s, a, z)^\top z\big] - H(\mu), \end{aligned}\]where $\mu$ is the policy distribution at each state and $H(\mu)$ is approximated via the log-sum exponential of $Q_z$.
Method
The ideal test-time objective can be written as
\[\max_\pi \mathbb{E}^{\pi} \left[ \sum_{t=0}^{\infty} \gamma^t R(s_t) - \lambda \max\left(\sum_{t=0}^{\infty} \gamma^t C(s_t) - \epsilon, 0\right) \right].\]For tractability, I instead optimize
\[\mathbb{E}^{\pi} \left[ \sum_{t=0}^{\infty} \gamma^t (R(s_t) - \lambda C(s_t)) \right]\]whenever the expected cost exceeds the threshold, and I use the original reward otherwise. Let $Q_{R}^\pi$ denote the standard Q-function and $Q_{C}^\pi$ the Q-function for the cost. The FB-safe objective becomes
\[\max_\pi \begin{cases} Q_{R - \lambda C}^\pi(s, a), & \text{if } Q_C^*(s, a) \ge \epsilon, \\ Q_R^\pi(s, a), & \text{if } Q_C^*(s, a) < \epsilon. \end{cases}\]The resulting optimal policies are
\[\begin{aligned} \pi_{R - \lambda C}^* &= \arg\max_\pi Q_{R - \lambda C}^\pi(s, a), \\ \pi_R^* &= \arg\max_\pi Q_R^\pi(s, a), \end{aligned}\]and they are combined into the FB-safe policy
\[\pi_{\text{safe}}(s) = \begin{cases} \pi_R^*(s), & \text{if } Q_C^*(s) \le \epsilon, \\ \pi_{R - \lambda C}^*(s), & \text{if } Q_C^*(s) > \epsilon. \end{cases}\]Given reward and cost samples, the latent vectors are
\[\begin{aligned} z_C &= \mathbb{E}_\rho[C(s) B(s)], \\ z_{R - \lambda C} &= \mathbb{E}_\rho[(R(s) - \lambda C(s)) B(s)]. \end{aligned}\]Using the pretrained FB framework, I compute $\pi^_{R-\lambda C},$ $\pi^R,$ and $Q^*_C,$ and select the appropriate policy. The policy $\pi^*{R-\lambda C}$ acts as a recovery controller that steers the agent back to the safe region. In practice I set
\[\lambda = \frac{\mathbb{E}_\rho[R(s)]}{\mathbb{E}_\rho[C(s)]}\]to balance reward maximization and cost minimization.
Experiments
I evaluate FB-safe on the DSRL benchmark (Liu et al., 2024), specifically the BulletSafetyGym environments (Gronauer and Diehl, 2022). I compare against recent offline safe RL baselines: BC-safe, CPQ (Xu et al., 2022), COptiDICE (Lee et al., 2022), and CDT (Liu et al., 2023). These methods are trained with access to reward and cost, while FB-safe is trained in a zero-shot fashion without either signal.
The normalized reward and cost follow the DSRL conventions. Cost values below one are considered safe. Each method is run with three seeds for 20 episodes at cost thresholds $\epsilon \in {10, 20, 40}$ and I report the average across all experiments.
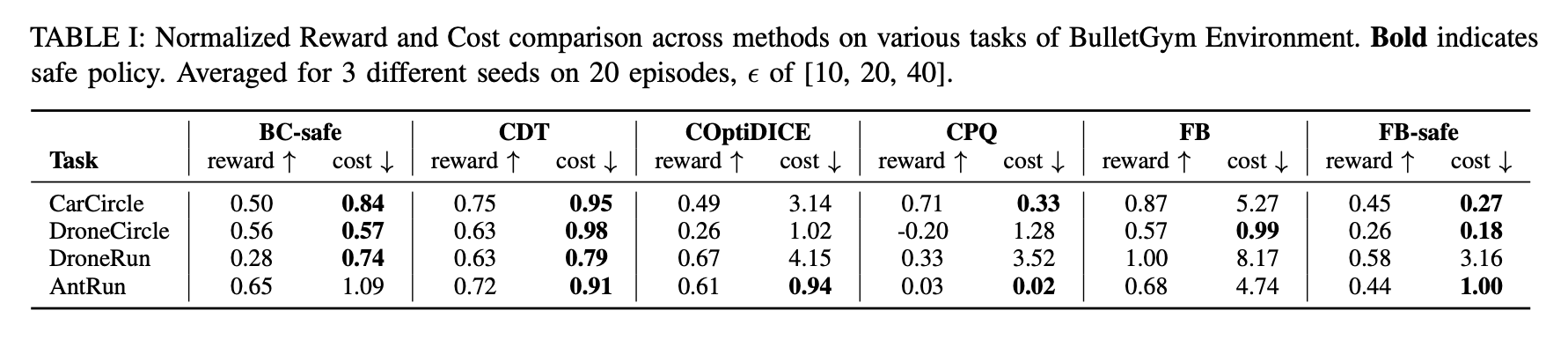
FB-safe achieves a competitive trade-off between reward maximization and cost minimization across multiple tasks. Compared to the vanilla FB policy, FB-safe significantly reduces cost, demonstrating that the safety-aware selection layer is effective even in the zero-shot setting.
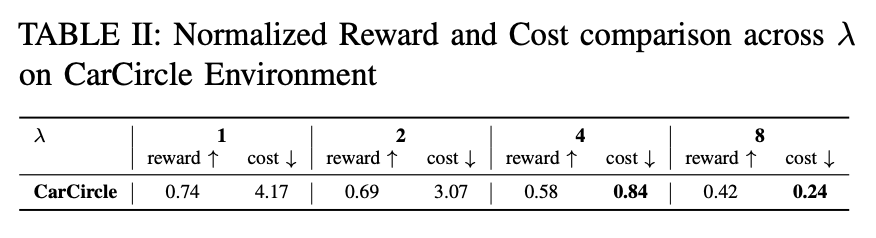
I further study the effect of the hyperparameter $\lambda$, which governs the trade-off between reward and safety. A small $\lambda$ fails to prevent risky behavior, while a larger $\lambda$ reduces cost at the expense of reward. Balancing this trade-off remains an important direction for future work.
Conclusion
I introduced FB-safe, a zero-shot safe RL framework that extends FB representations with a safety-aware policy selection mechanism. FB-safe balances reward and cost in offline safe RL environments without relying on reward or cost signals during training. Experiments on the DSRL benchmark show that FB-safe matches or outperforms existing offline safe RL baselines in cost reduction, despite operating in a more challenging zero-shot setting.
This approach can be applied when cost functions are defined dynamically, making it suitable for domains where explicit safety signals are hard to obtain. Future work will extend FB-safe to pixel-based state representations and natural-language safety constraints, enabling richer generalization and explainability in real-world deployment scenarios.
A current limitation is that performance is sensitive to the choice of $\lambda$, which I treat as a fixed hyperparameter. Developing adaptive strategies for tuning $\lambda$ is a promising direction for improving the balance between performance and safety.
By addressing these avenues, FB-safe can provide a robust foundation for safe, generalizable, and interpretable reinforcement learning systems, especially for robotics and autonomous navigation in environments with dynamic and complex safety requirements.